Ngoài việc đam mê về business, mình còn sở thích là toán học. Mình hay nghiên cứu giải các bài toán hình học, xác suất và số học. Gần đây mình đã giải bài toán Routh. Quá trình giải tuy mất nhiều thời gian, nhưng mình rút ra một số phương pháp giải quyết vấn đề trong cuộc sống.
1/ Bài toán càng tổng quát, càng khó giải. Bài toán càng chi tiết, càng dễ giải.
=> Nguyên nhân: Với bài toán tổng quát, bạn phải tìm ra quy luật bất biến trong sự biến đổi; sau đó chứng minh quy luật này là đúng.
Bài toán chi tiết vs Bài toán tổng quát
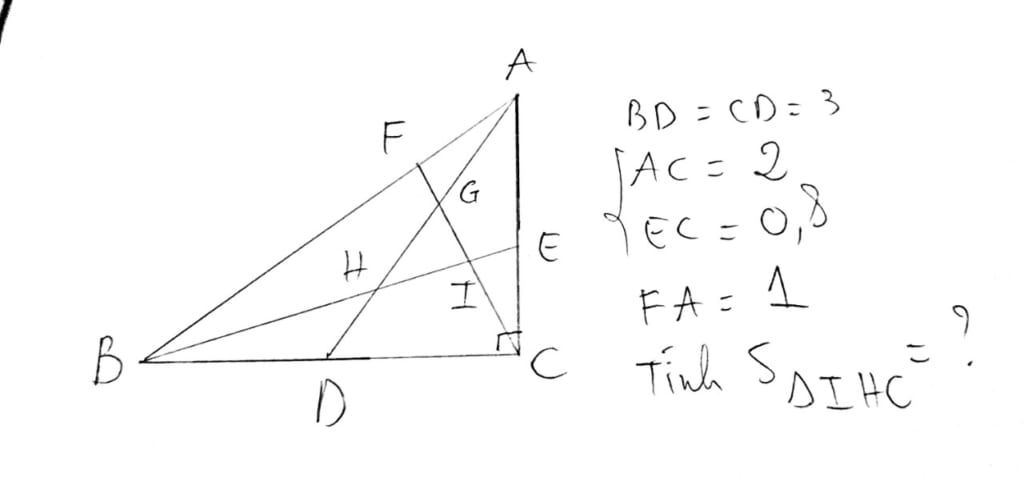
Bài toán tổng quát cho lại kết quả có thể ứng dụng rộng hơn bài toán với phạm vi hẹp
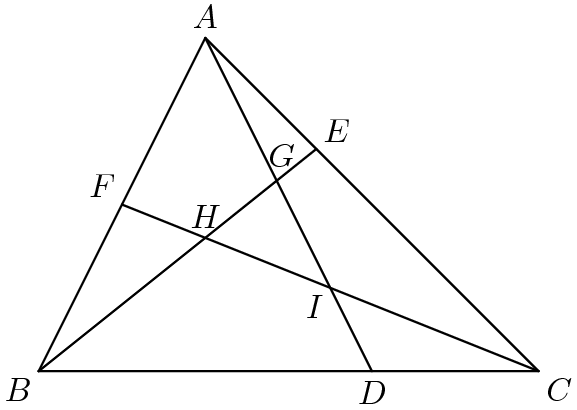
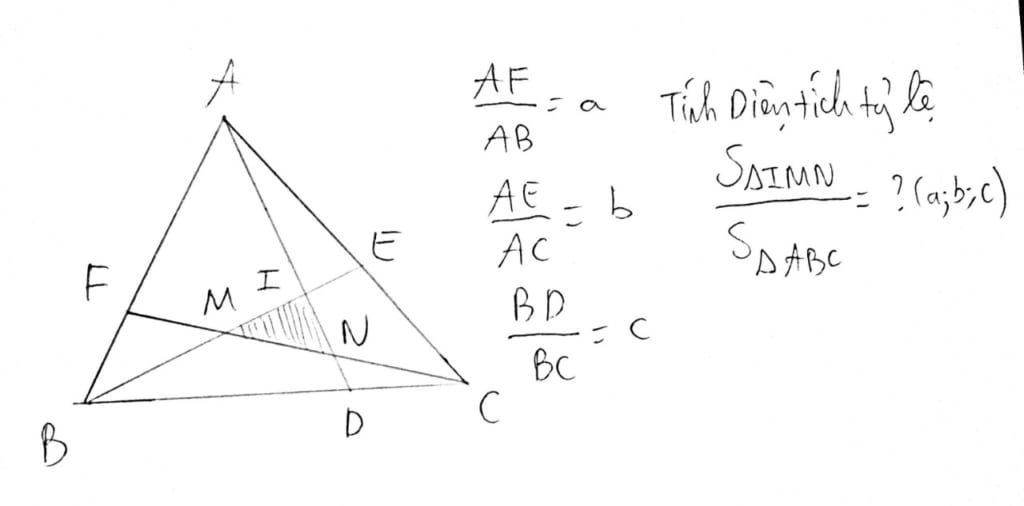
2/ Chia nhỏ vấn đề
Mọi bài toán phức tạp đều có thể chia tách thành những bài toán con “cơ bản” hơn. Kết quả của những bài toán “cơ bản” sẽ dùng để giải quyết bài toán lớn.
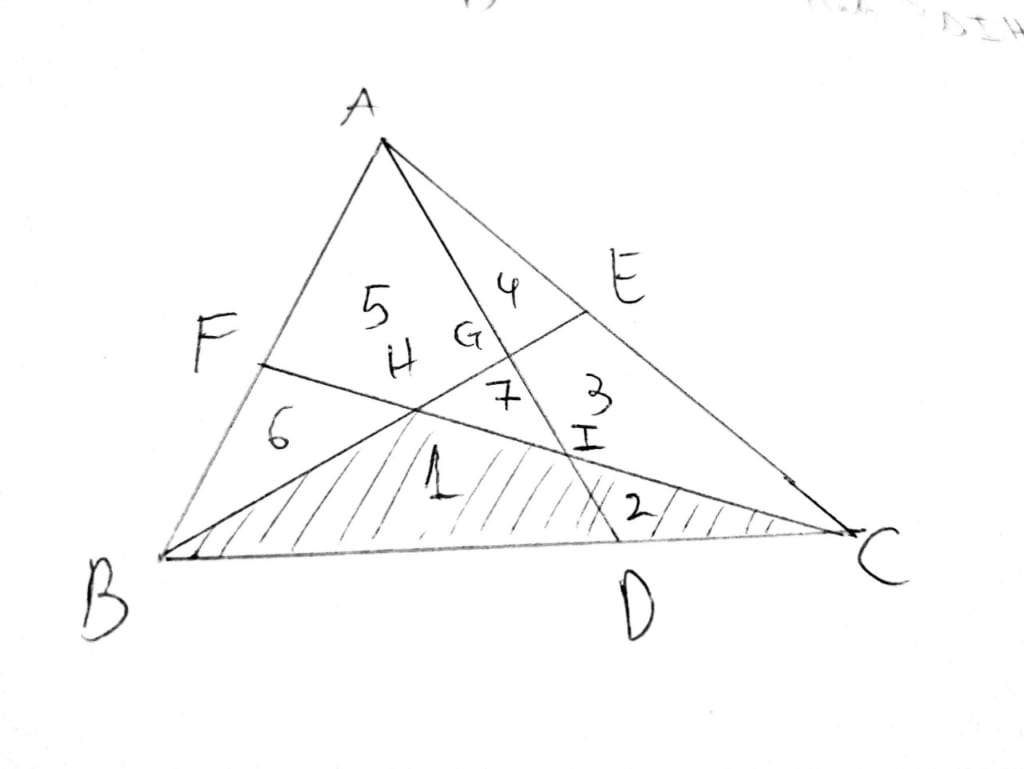
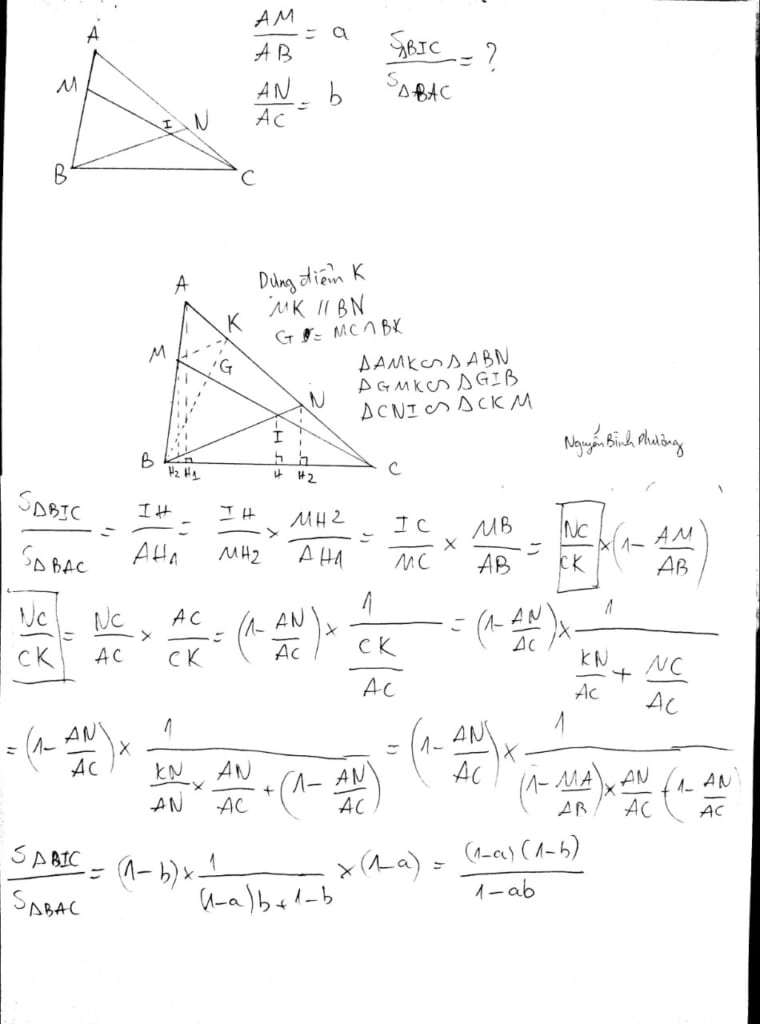
Chia tách thành 2 bài toán: Bài toán 1: Tính diện tích tam giác ABC trừ đi các phần (1), (2), (3), (4), (5), (6). Bài toán 2: Tính tỷ lệ diện tích tam giác BHC/ Tam giác ABC

Xem xét ở trường hợp lý tưởng, trường hợp đơn giản đặc biệt. Giải quyết vấn đề ở trường hợp lý tưởng này. Đây là cách để tìm ra bài toán dễ hơn, làm tiền đề, gợi mở cách tiếp cận cho bài toán phức tạp.
Để giải bài toán 2: Mình suy nghĩ bằng cách đưa về tình huống lý tưởng: FE//BC (song song) và BC vuông góc với AC. Mình thử cho giá trị của BC và AC, giá trị của a và b. Mình cố gắng giải bài toán ở trường hợp đặc biệt (đơn giản hơn). Sau khi đã giải bài toán "ở trường hợp đặc biệt", mình quay về dạng tổng quát hóa.
3/ “Cơ bản” nhưng không phải “luôn dễ”. Simple but not easy.
Trong quá trình giải toán, những bước suy luận chuyển tiếp càng “cơ bản”, thì quá trình suy luận càng chắc chắn. Những bước suy luận nhảy cóc “cao siêu” khiến bạn không hiểu rõ tường tận, rất có thể là bước suy luận sai. Mỗi công thức chỉ đúng trong scope nhất định, có thể trường hợp bạn dùng lại không thuộc scope khả dĩ.
4/ Giải toán gồm 3 việc chính
A. Chia tách, tổng hợp các định lý nhỏ (bài toán nhỏ)
B. Tìm ra quy luật bất biến, điều là điểm chung, là sợi dây liên kết bất biến của sự biến đổi.
C. Xây dựng/tìm kiếm đối tượng trung gian hoặc hệ quy chiều liên kết những sự khác biệt (thậm chí đối lập) về cùng 1 hệ quy chiếu
Bài toán 2 thật sự rất khó giải Cái khó là mình không thể liên kết mối quan hệ giữa HN, BF và EC. Do đó, mình dựng đường phụ FQ//BE. Ta có: a = AF/AB = AQ/AE b = AE/AC CE/CQ = HE/FQ = HC/FC = HN/FP Từ đó, ta có thể tìm được lời giải Đường FQ là chiều khóa liên kết tỷ số a và b. FQ giúp ta đưa về 1 hệ quy chiếu là đường AC (A, Q, E, C)
Bài học rút ra: Trong cuộc sống, khi ta gặp dilemma a và b. Chọn a hoặc chọn b đều không ổn. Ta nên đưa về 1 hệ quy chiếu c cùng kết nối a và b. Cùng đặt a và b trong 1 bức tranh tổng c và có sự liên hết chặt chẽ.
Khi nhìn vào c (chứa a và b), bạn sẽ không còn chỉ thấy a hoặc b riêng lẻ.
5/ Sự liên kết chặt chẽ là những sự liên kết “cơ bản”
Những bước chuyển “cao siêu” đúng thì đều có thể giải thích bằng những (dù rất nhiều) những bước suy luận “cơ bản”, có “luận cứ” rõ ràng. Đừng để những “opinion” cao siêu, những nhận định chủ quan, hay những điều phức tạp, khó hiểu làm che mờ sự thật. Nếu chúng là sự thật, thì chắc chắn chúng cỏ thể được chứng minh bằng những điều “căn bản”.
6/ Những cách phổ biến để giải quyết sự đối lập, tìm điểm cân bằng hoặc kết nối những điều có vẻ không liên quan nhau
A và B
Mối liên hệ bắc cầu. (A liên hệ C); (B liên hệ C) => A liên hệ B
Bức tranh tổng. (A thuộc C); (B thuộc C) => A và B đều thuộc C
Đối tượng tương đồng. Tạo A’. Tìm mối quan hệ A’ và B
Tập hợp con. C là tập hợp con giao giữa A và B
Đặt trên 1 hệ quy chiếu. Lượng hóa A và B trên hệ trục tọa độ Đề-cat (cùng hệ quy chiếu)
